Vector Space

Consider a vector $\vec{v}\in\mathbb{R}^d$, here $\vec{v}$ lives in $d$ dimensional space this space is a vector space.

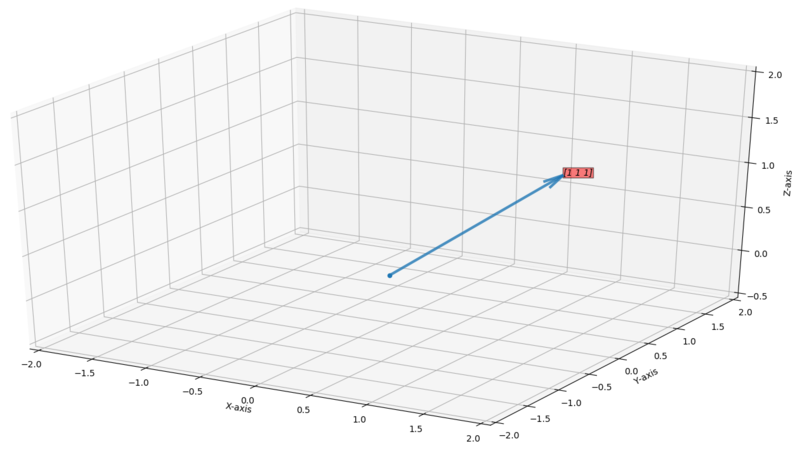
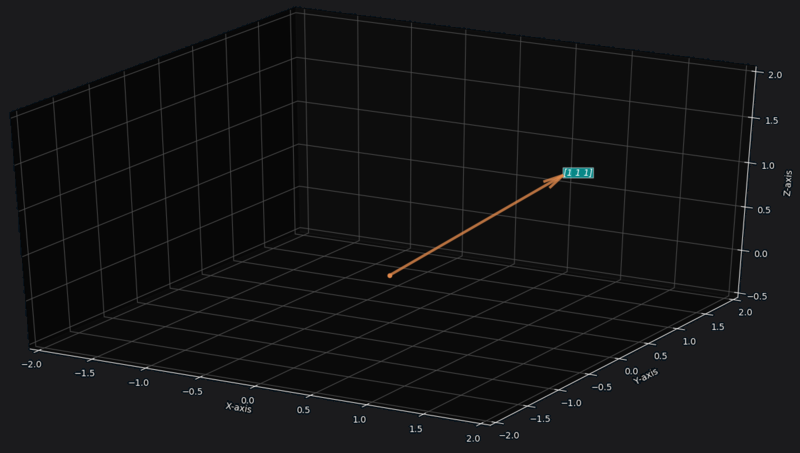
For example, for $d=3$,

Code to plot this vector (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt
m = mvar.MultiVariable()
vector = np.array([[1, 1, 1]])
m.plot_3D_vectors(vector)
## Adjusting axis limits
m.set_axes_limit((-2, 2))
m.setZ_limit((-0.5, 2))

Download MultiVariable class ⬇

Vector shown in the blue is a vector $\vec{x}\in\mathbb{R}^3$. All the space surrounding this vector is $3$-dimensional vector space.

If we multiply a vector $\vec{v}$ by a constant say $c$ then the resulting vector is in the direction of $\vec{v}$ (or in opposite direction).
Say the resulting vector is $\vec{v}'$ then we can say that $\vec{v}' = c \vec{v}$ where $c\in\mathbb{R}$, it is a line along vector $\vec{v}$.
Here you can see that $\vec{v}'$ has it's own space inside that $d$ dimensional space, it's a vector space inside a vector space.
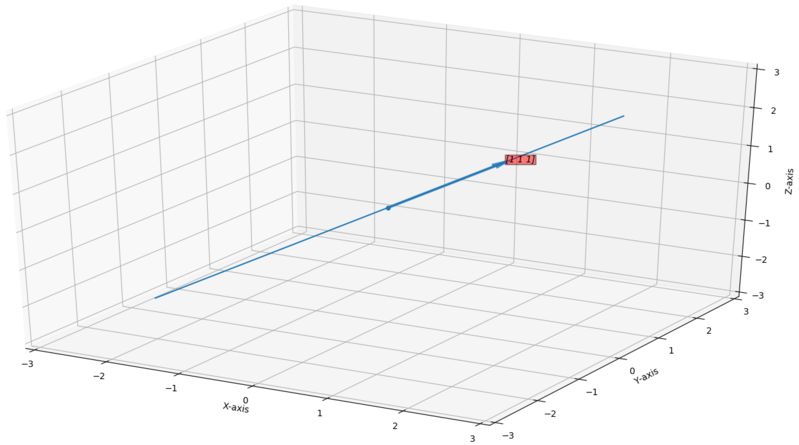
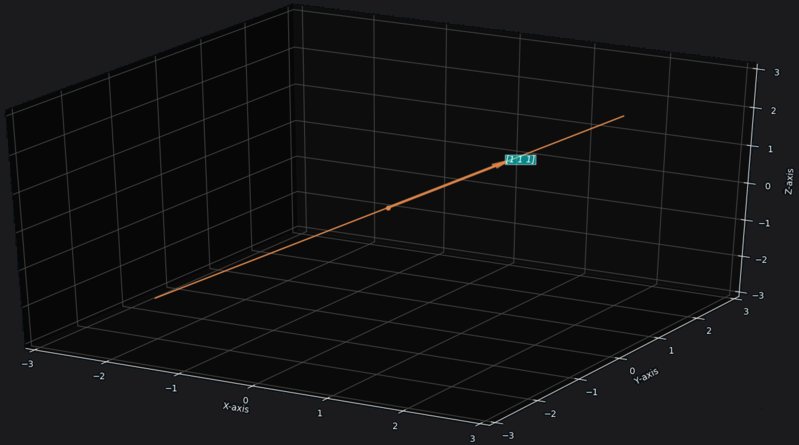
Example for $d=3$

Code to plot this vector (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt
m = mvar.MultiVariable()
## Here line is defines as [x-start, x-end, y-start, y-end, z-start, z-end]
lines = np.array([[-2, 2, -2, 2, -2, 2]])
m.plot_3D_lines(lines)
vector = np.array([[1, 1, 1]])
m.plot_3D_vectors(vector, plot_separately=False)
## Adjusting axis limits
m.set_axes_limit((-3, 3))

Download MultiVariable class ⬇

Here you can see the vector $\vec x\in\mathbb R^3$ has it's own vector space that is that line.

Now Consider a plane(passing through origin) inside a $3$-dimensional space, this plane lives inside $3$-dimensional vector space, but it has it's own vector space.

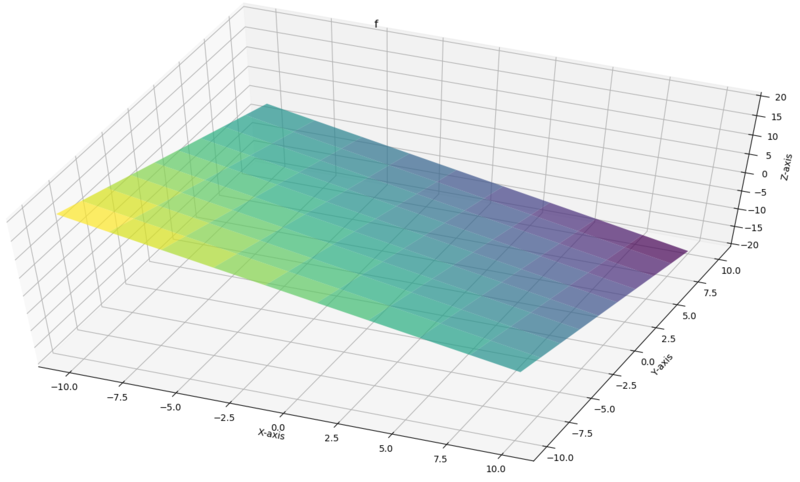
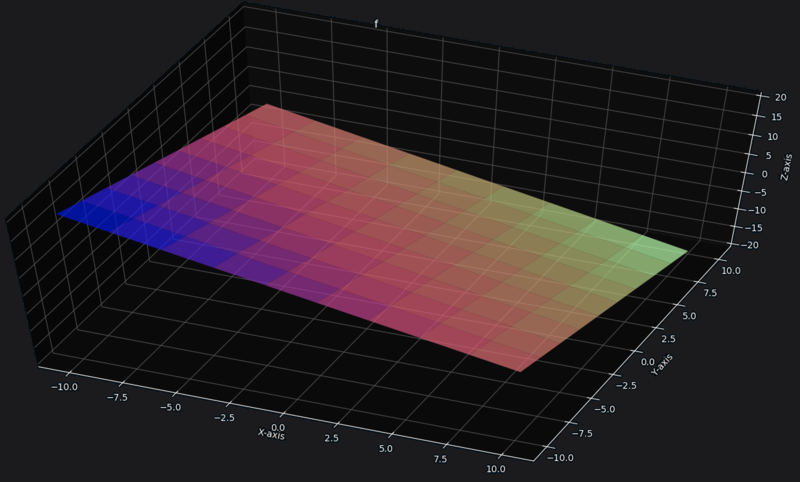
Code to plot this plane (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt

def f(x,y):
    return -x -y

m = mvar.MultiVariable()
m.plot_surface_color_3D(f, plot_separately=True, alpha=0.7)

Download MultiVariable class ⬇

Here you can see the plane $x+y+z=0$ has it's own vector space inside $3$-dimensional vector space.

If we add any two $d$-dimensional vectors, we get a $d$-dimensional vector as a output.
Say we have two vectors $\vec{v}\in\mathbb{R}^d$ and $\vec{w}\in\mathbb{R}^d$, then if we take there linear combination, then that linear combination will have it's own vector space, but what that vector space looks like?
Well it depends, on how $\vec{v}$ and $\vec{w}$ are oriented.

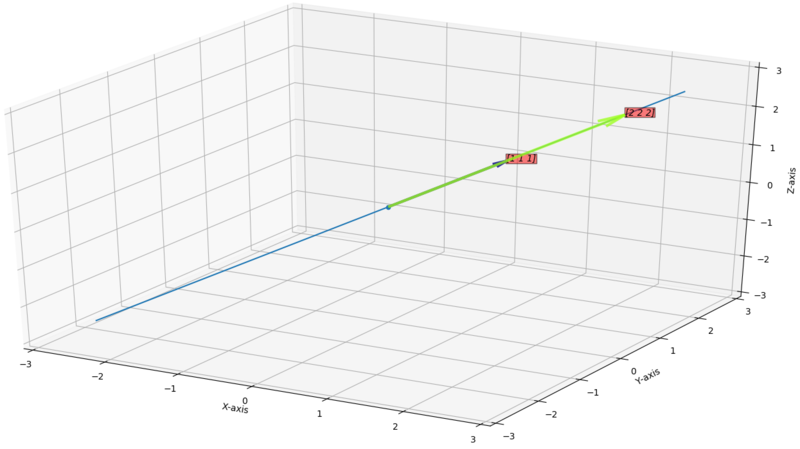
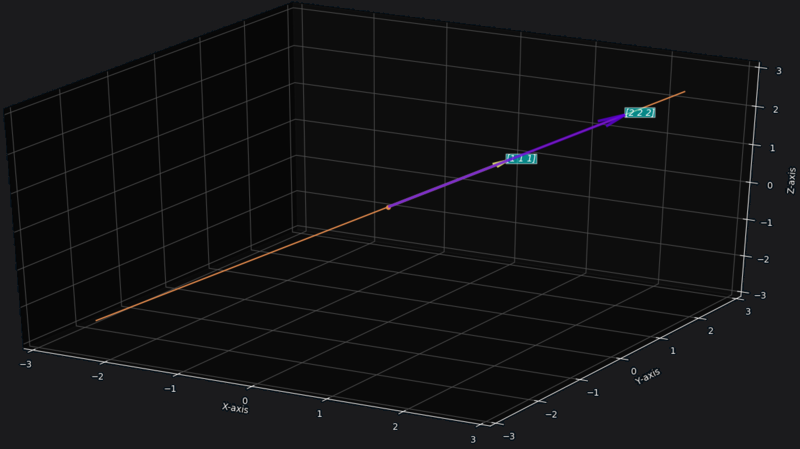
Case 1: if $\vec{v}$ is parallel to $\vec{w}$
If $\vec{v}$ and $\vec{w}$ are parallel then $\vec{w}= c \vec{v};\quad c\in\mathbb{R}$, So vector space is just a line.
Example for $d=3$:
Say the vectors are,

$$\vec{v} = \begin{bmatrix} 1 \\ 1\\ 1\\ \end{bmatrix} \text{ and } \vec{w} = \begin{bmatrix} 2 \\ 2\\ 2\\ \end{bmatrix}$$

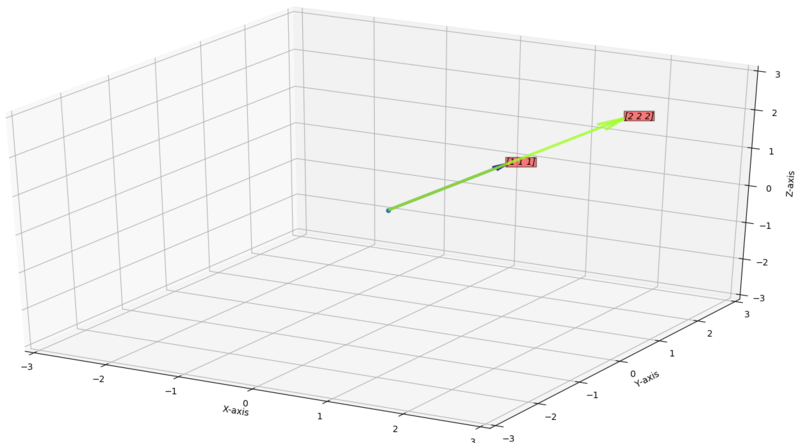
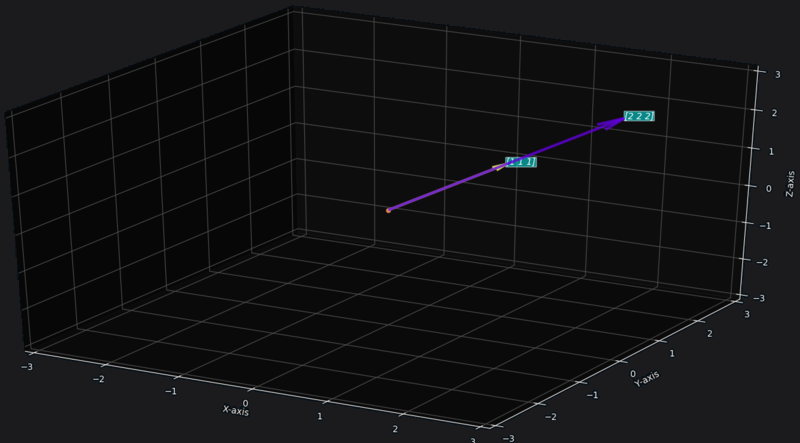
Then the vector space is just a line passing through these vectors.

Code To plot this (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt

m = mvar.MultiVariable()
vectors = np.array([
                    [1, 1, 1],
                    [2, 2, 2]
                   ])
origin = np.array([0, 0, 0])
m.plot_3D_vectors(vectors, origin, plot_separately=False)

# Structure of lines = [[x-start, x-end, y-start, y-end, z-start, z-end],...]
lines = np.array([
    [-2.5, 2.5, -2.5, 2.5, -2.5, 2.5]
])
m.plot_3D_lines(lines, plot_separately=False)
m.set_axes_limit((-3, 3))

Download MultiVariable class ⬇

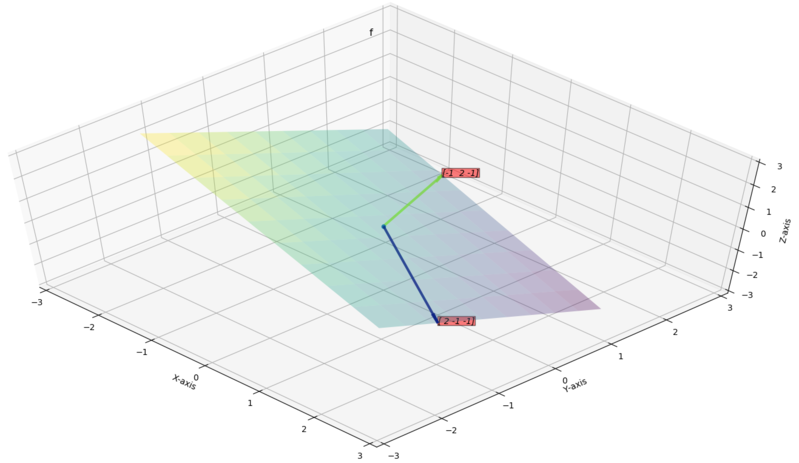
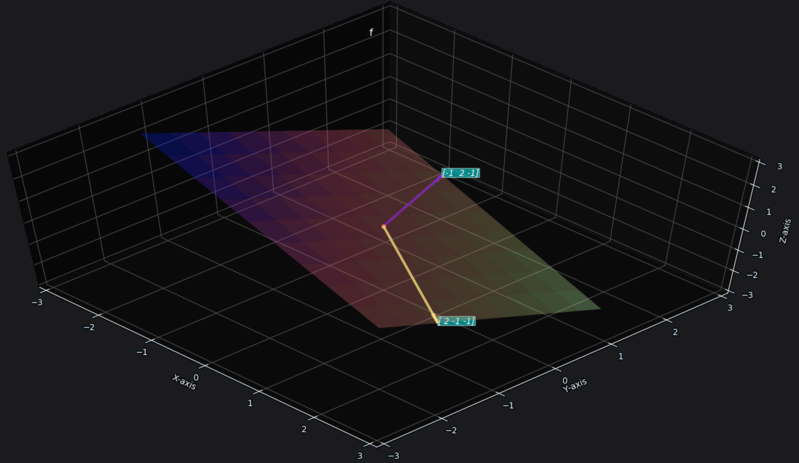
Case 2: if $\vec{v}$ is not parallel to $\vec{w}$
If $\vec{v}$ and $\vec{w}$ are not parallel then the vector space of linear combination of $\vec{v}$ and $\vec{w}$ is a plane.
Example for $d=3$:
Say the vectors are,

$$\vec{v} = \begin{bmatrix} 2 \\ -1\\ -1\\ \end{bmatrix} \text{ and } \vec{w} = \begin{bmatrix} -1 \\ 2\\ -1\\ \end{bmatrix}$$

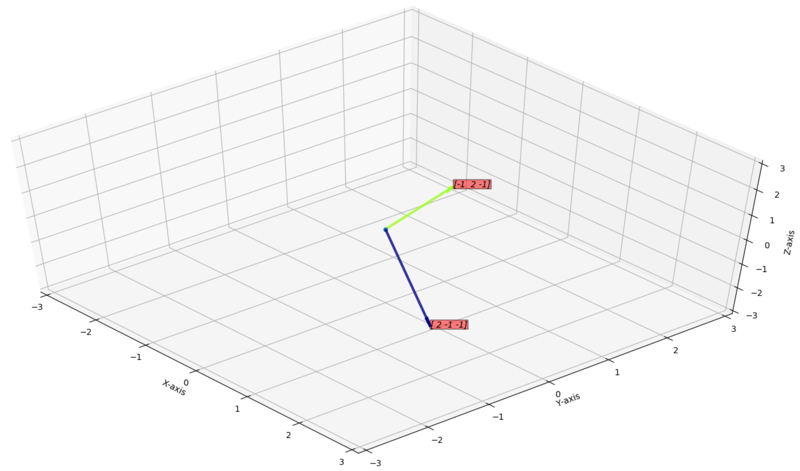
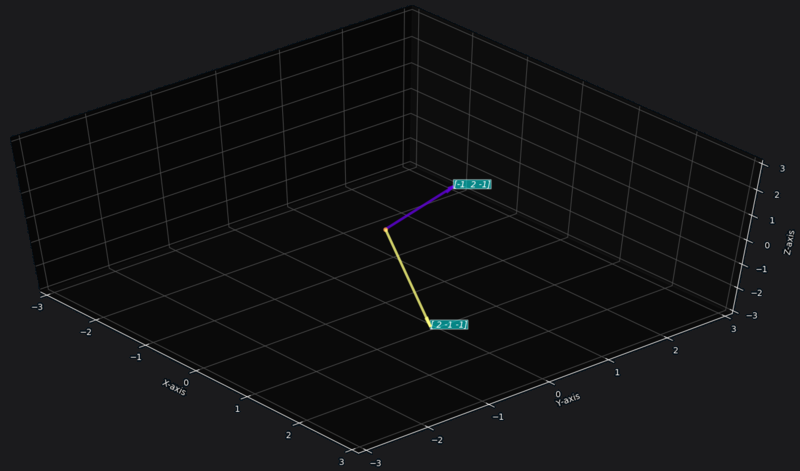
Then the vector space is the plane passing through these vectors (shown below).

Code To plot this (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt

# X + Y + Z = 0
def f(x,y):
    return -x -y

m = mvar.MultiVariable(count = 10, x_range=(-2,2), y_range=(-2,2), z_range=(-2,2))
vectors = np.array([
                    [2,-1,-1],
                    [-1,2,-1]
                   ])
origin = np.array([0,0,0])
m.plot_3D_vectors(vectors, origin, plot_separately=False)
m.plot_surface_lines_3d(f, density = 100, plot_separately=False)
m.set_axes_limit((-3,3))

Download MultiVariable class ⬇

Vector Space Properties

So when can we say that a space can be a vector space?
A space is a vector space if it full fill these conditions:

• If there is a vector in this space and we multiply that vector with a constant $c\in\mathbb{R}$ then the resulting vector must be in the space.
• Say we took two vectors $\vec{v}$ and $\vec{w}$ then there sum must be in this space.

Let's see an example of a space which is not a vector space.
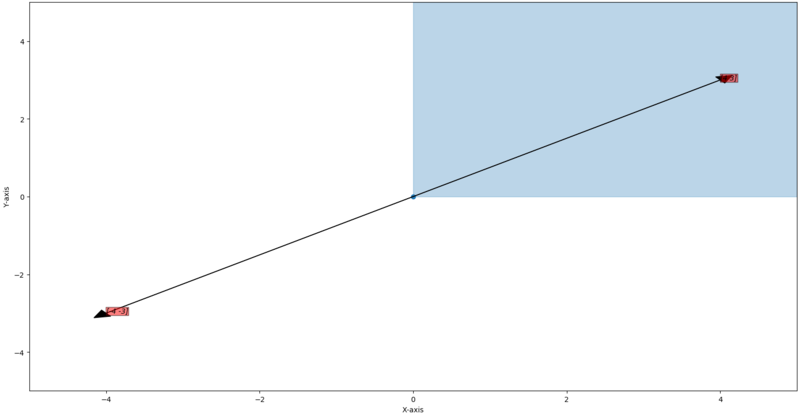
Think of a 2 dimensional space where $x\gt0$ and $y\gt0$

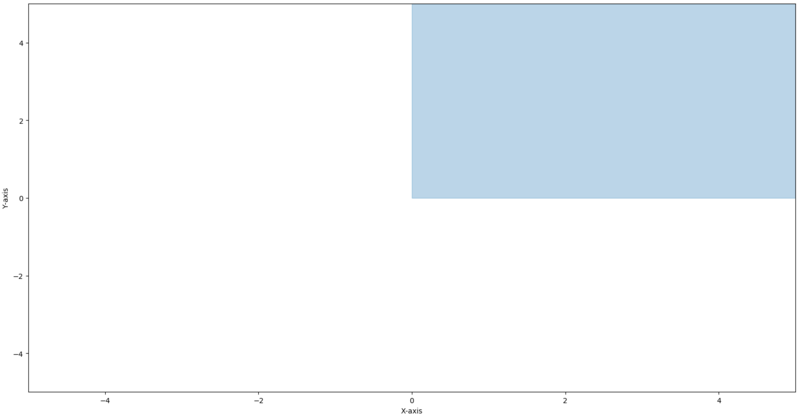
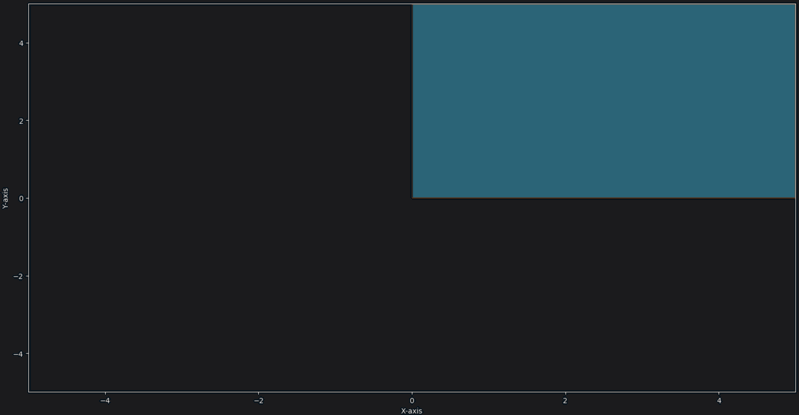
We can add vector safely and we don't go out of the space.
What about multiplying a constant to a vector, take a vector in that space $\vec{v}=\begin{bmatrix} 4 \\ 3\\ \end{bmatrix}$.

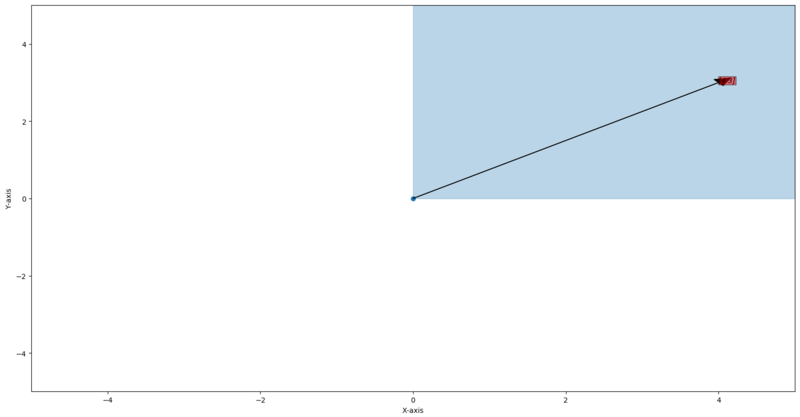
if we multiply $\vec{v}$ by $-1$ then if goes out of space.

Code To plot this (python)

import MultiVariable as mvar
import numpy as np
%matplotlib qt

m = mvar.MultiVariable()

x = np.array([0,  5])
y1 = np.array([5,5])
y2 = np.array([0, 0])
m.fill_between(x, y1, y2, alpha=0.3)

vectors = np.array([
                    [4,3],
                    [-4,-3],
                   ])
origin = np.array([0,0])
m.plot_2D_vectors(vectors, origin, plot_separately=False, head_width=0.2, head_length=0.2)
m.set_axes_limit((-5,5))

Download MultiVariable class ⬇

So it can't be a vector space.

info

A vector space must pass through the origin.

Vector space inside a vector space is referred as a subspace.
Possible subspace of a $2$-dimensional space.

• All $\mathbb{R}^2$ space
• All lines passing through origin.
• Origin itself ($\vec{0}$)