Singular Value Decomposition

note

Previously we have seen that for $n\times n$ matrix (say$A$) with $n$ independent eigenvectors factorization is,

$$\begin{matrix} A=S\Lambda S^{-1} \end{matrix}$$

Previously we have seen that if eigenvectors of matrix $A$ are orthogonal then $Q^{-1}=Q^T$, then the factorization is,
(We discussed it in detail HERE)

$$\begin{matrix} A=Q\Lambda Q^{T} \end{matrix}$$

But generally eigenvectors are not orthogonal.

Singular Value Decomposition(SVD) is a factorization of any $m\times n$ matrix.

danger

$$\begin{matrix} A=U\Sigma V^T \end{matrix}$$

Say that we have a $m\times n$ matrix $A$ and $\text{Rank}(A)=r$,

$$A_{m\times n}=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix}$$

info

IDEA: behind SVD is to map an orthonormal basis in $\mathbb{R}^n$ (Row space + Null Space of matrix $A^TA$) to the orthonormal basis in $\mathbb{R}^m$ (Column space + Left Null Space of matrix $AA^T$).

$\quad$

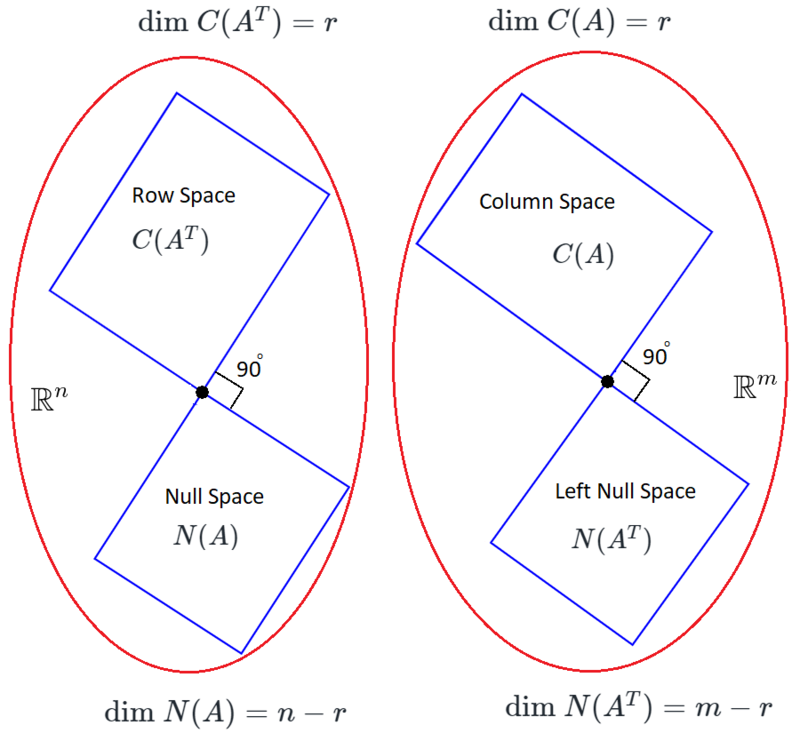
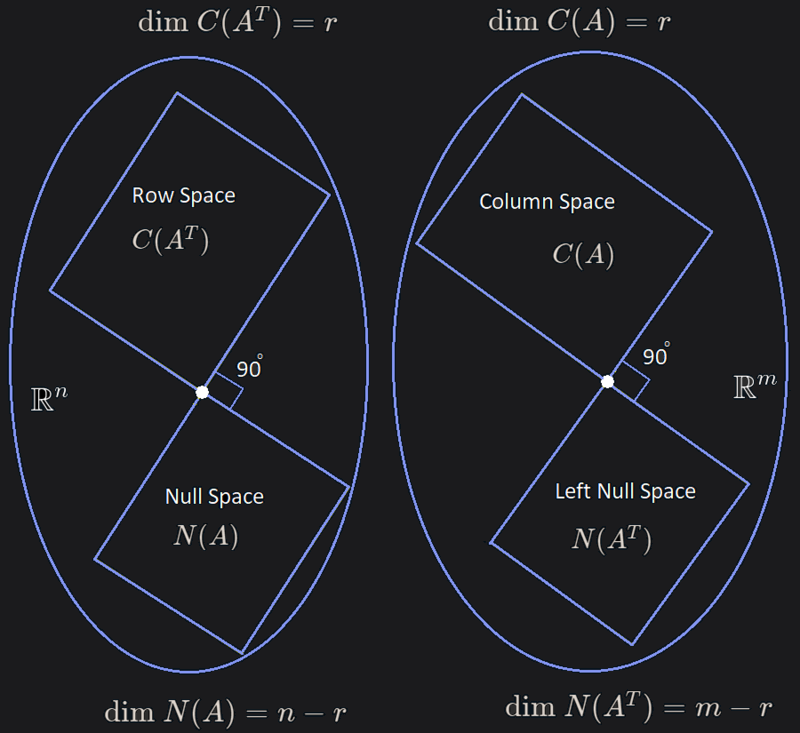
The row space is in $\mathbb{R}^n$, here our row vectors are,

$$\begin{bmatrix} a_{11} \\ a_{12} \\ \vdots \\ a_{1n} \end{bmatrix}\in\mathbb{R}^n, \begin{bmatrix} a_{21} \\ a_{22} \\ \vdots \\ a_{2n} \end{bmatrix}\in\mathbb{R}^n, \cdots, \begin{bmatrix} a_{m1} \\ a_{m2} \\ \vdots \\ a_{mn} \end{bmatrix}\in\mathbb{R}^n$$

The column space is in $\mathbb{R}^m$, our column vectors are,

$$\begin{bmatrix} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \end{bmatrix}\in\mathbb{R}^m, \begin{bmatrix} a_{12} \\ a_{22} \\ \vdots \\ a_{m2} \end{bmatrix}\in\mathbb{R}^m, \cdots, \begin{bmatrix} a_{1n} \\ a_{2n} \\ \vdots \\ a_{mn} \end{bmatrix}\in\mathbb{R}^m$$

A vector (say) $\vec{v}\in\mathbb{R}^n$ has some portion in Row Space and some in Left Null Space, when we transform that vector $\vec{v}\in\mathbb{R}^n$ using matrix $A$, $A\vec{v}=\vec{u}\in\mathbb{R}^m$ now this vector $\vec{u}\in\mathbb{R}^m$ has some portion in Column Space and some in Null Space
$\vec{u}=\vec{u}_p+\vec{u}_n$ [Reference]

● Row space $(C(A^T))$ (Gather Orthonormal Basis vectors for Row Space)

note

Row vectors lives in $n$-dimensional vector space.
$\text{Rank}(A)=r$ so we have $r$ independent row vectors.
So the space spanned by row vectors is $r$-dimensional vector space(Row Space), so to span this whole $r$-dimensional vector space we need $r$ independent basis vectors.
Among those we choose orthonormal basis vectors.

( we can get them using Gram Schmidt method, but here we will use $A^TA$ to get them we will discuss it below)
(say) our orthonormal basis vector for Row Space are $\vec{v}_1,\vec{v}_2,\cdots,\vec{v}_r$.

● Null Space $(N(A))$ (Orthonormal Basis vectors of Null Space)

note

Null Space is perpendicular to Row Space(we talked about orthogonal subspaces HERE), so every vector in Null Space is perpendicular to Row Space.
$\text{Rank}(A)=r$ so we have $n-r$ dependent(free) row vectors.
So the space spanned by vectors in Null Space is $(n-r)$-dimensional vector space(Null Space), so to span this whole $(n-r)$-dimensional vector space we need $n-r$ independent basis vectors in Null Space.
(we don't need to find basis vectors for SVD we discuss it below in Column Space$(C(A))$ section )
(say) our orthonormal basis vector for Null Space are $\vec{v}_{r+1},\vec{v}_{r+2},\cdots,\vec{v}_n$.

● Column Space $(C(A))$ (Map the Orthonormal Basis vectors from the Row Space to Column Space)

note

After we got our orthonormal basis vector for Row Space $\vec{v}_1,\vec{v}_2,\cdots,\vec{v}_n$, we map them to the Column Space using matrix $A$.
$\text{Rank}(A)=r$ so,

$$\begin{matrix} A\vec{v}_i=\sigma_i\vec{u}_i;\quad\forall i\in\{1,2,\cdots,r\} \end{matrix}$$

For $i\in\{1,2,\cdots,r\}$ $A$ maps $\vec{v}_i$ to $\sigma_i\vec{u}_i$ then we normalize it to get $\vec{u}_i$(unit vector), $\sigma_i$ is the length of $A\vec{v}_i$.
Now we got the orthonormal basis vector for our column space $\vec{u}_1,\vec{u}_2,\cdots,\vec{u}_r$

$$\begin{matrix} A\vec{v}_i=\vec{0};\quad\forall i\in\{r+1,r+2,\cdots,n\} \end{matrix}$$

For $i\in\{r+1,r+2,\cdots,n\}$ $\vec{v}_i$ lives in the Null Space of $A$
So $\vec{u}_{r+1},\vec{u}_{r+2},\cdots,\vec{u}_n$ are all $\vec{0}$

But wait WHY all $\vec{u}_i$'s are perpendicular to each other?
we discussed it below in $A^TA$ section.

● Left Null Space $(N(A^T))$ (Map the Orthonormal Basis vectors from the Null Space to Left Null Space)

note

Left Null Space is perpendicular to Column Space(we talked about orthogonal subspaces HERE), so every vector in Left Null Space is perpendicular to Column Space.
$\text{Rank}(A)=r$ so we have $m-r$ dependent(free) column vectors.
So the space spanned by vectors in Left Null Space is $(m-r)$-dimensional vector space(Null Space), so to span this whole $(m-r)$-dimensional vector space we need $m-r$ independent basis vectors in Left Null Space.
(say) our orthonormal basis vector for Left Null Space are $\vec{u}_{r+1},\vec{u}_{r+2},\cdots,\vec{u}_n$.

● Terminologies
Say $\vec{v}_1,\vec{v}_2,\cdots,\vec{v}_r$ are Orthonormal Basis vectors for Row Space $(C(A^T))$,
and $\vec{v}_{r+1},\vec{v}_{r+2},\cdots,\vec{v}_n$ are Orthonormal Basis vectors for Null Space $(N(A^T))$

$$\text{(say)} \mathbf{V}'= \begin{bmatrix} \begin{matrix} \vdots & \vdots & & \vdots \\ \vec{v}_1 & \vec{v}_2 & \cdots & \vec{v}_r \\ \vdots & \vdots & & \vdots \end{matrix} & \begin{matrix} \vdots & \vdots & & \vdots \\ \vec{v}_{r+1} & \vec{v}_{r+2} & \cdots & \vec{v}_n \\ \vdots & \vdots & & \vdots \end{matrix} \end{bmatrix}_{n\times n} \\ \text{(say)} \mathbf{U}'= \begin{bmatrix} \begin{matrix} \vdots & \vdots & & \vdots \\ \vec{u}_1 & \vec{u}_2 & \cdots & \vec{u}_r \\ \vdots & \vdots & & \vdots \end{matrix} & \begin{matrix} \vdots & \vdots & & \vdots \\ \vec{u}_{r+1} & \vec{u}_{r+2} & \cdots & \vec{u}_n \\ \underbrace{\vdots}_{=\vec{0}} & \underbrace{\vdots}_{=\vec{0}} & & \underbrace{\vdots}_{=\vec{0}} \end{matrix} \end{bmatrix}_{m\times n} \\ \text{(say)} \Sigma'= \begin{bmatrix} \begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_r \\ \end {bmatrix}_{r\times r} & \mathbf{0}_{r\times (n-r)} \\ \mathbf{0}_{(n-r)\times r} & \mathbf{0}_{(n-r)\times (n-r)} \end{bmatrix}_{n\times n}$$

Mapping from $\mathbb{R}^n$ to $\mathbb{R}^m$ is,

danger

$$\begin{matrix} A\vec{v}_i=\sigma_i\vec{u}_i;\quad\forall i\in\{1,2,\cdots,n\} \end{matrix}$$

We can Write it as,

$$A\underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{v}_1 & \vec{v}_2 & \cdots & \vec{v}_n \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ V'_{_{n\times n}} } = \underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{u}_1 & \vec{u}_2 & \cdots & \vec{u}_n \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ U'_{m\times n} } \underbrace{\begin{bmatrix} \begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_r \\ \end {bmatrix}_{r\times r} & \mathbf{0}_{r\times (n-r)} \\ \mathbf{0}_{(n-r)\times r} & \mathbf{0}_{(n-r)\times (n-r)} \end {bmatrix}}_{ \Sigma'_{n\times n} }$$

So,

$$AV'_{n\times n}=U'_{m\times n}\Sigma'_{n\times n}$$

Full SVD

Say that all columns of our matrix $A$ are independent $\Rightarrow \text{Rank}(A)=m$, so

• Dimension of Row Space is: $m$

• Dimension of Null Space is: $n-m$

• Dimension of Column Space is: $m$

• Dimension of Left Null Space is: $m-m=0$ Our equation was,

  $$A\underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{v}_1 & \vec{v}_2 & \cdots & \vec{v}_n \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ V'_{_{n\times n}} } = \underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{u}_1 & \vec{u}_2 & \cdots & \vec{u}_n \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ U'_{m\times n} } \underbrace{\begin{bmatrix} \begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m \\ \end {bmatrix}_{m\times m} & \mathbf{0}_{m\times (n-m)} \\ \mathbf{0}_{(n-m)\times m} & \mathbf{0}_{(n-m)\times (n-m)} \end {bmatrix}}_{ \Sigma'_{n\times n} }$$

  So,

  $$AV'_{n\times n}=U'_{m\times n}\Sigma'_{n\times n}$$

  And as we discussed above that $\vec{u}_{r+1},\vec{u}_{r+2},\cdots,\vec{u}_n$ are all $\vec{0}$, so we can discard those vectors from our equation so now our equation will become,

  $$A\underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{v}_1 & \vec{v}_2 & \cdots & \vec{v}_n \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ V_{_{n\times n}} } = \underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{u}_1 & \vec{u}_2 & \cdots & \vec{u}_m \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ U_{m\times m} } \underbrace{\begin{bmatrix} \begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m \\ \end {bmatrix}_{m\times m} & \mathbf{0}_{m\times (n-m)} \end {bmatrix}}_{ \Sigma_{m\times n} }$$

  So,

  $$\begin{matrix} A_{m\times n}V_{n\times n}=U_{m\times m}\Sigma_{m\times n} \end{matrix}$$

  This equation is what we call Full SVD

Reduced SVD

If some of the columns of our matrix $A$ are dependent and say $\text{Rank}(A)=r$, so

• Dimension of Row Space is: $r$

• Dimension of Null Space is: $n-r$

• Dimension of Column Space is: $r$

• Dimension of Left Null Space is: $m-r$ Our equation was,

  $$A\underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{v}_1 & \vec{v}_2 & \cdots & \vec{v}_n \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ V'_{_{n\times n}} } = \underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{u}_1 & \vec{u}_2 & \cdots & \vec{u}_n \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ U'_{m\times n} } \underbrace{\begin{bmatrix} \begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m \\ \end {bmatrix}_{m\times m} & \mathbf{0}_{m\times (n-m)} \\ \mathbf{0}_{(n-m)\times m} & \mathbf{0}_{(n-m)\times (n-m)} \end {bmatrix}}_{ \Sigma'_{n\times n} }$$

  So,

  $$AV'_{n\times n}=U'_{m\times n}\Sigma'_{n\times n}$$

  And as we discussed above that $\vec{v}_{r+1},\vec{u}_{r+2},\cdots,\vec{u}_n$ are all $\vec{0}$, so these vectors are redundant we can discard those vectors from our equation so now our equation will become,

  $$A\underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{v}_1 & \vec{v}_2 & \cdots & \vec{v}_r \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ V_{_{n\times r}} } = \underbrace{\begin{bmatrix} \vdots & \vdots & & \vdots \\ \vec{u}_1 & \vec{u}_2 & \cdots & \vec{u}_r \\ \vdots & \vdots & & \vdots \end{bmatrix}}_{ U_{m\times r} } \underbrace{\begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_r \\ \end {bmatrix}}_{ \Sigma_{r\times r} }$$

  So,

  $$\begin{matrix} A_{m\times n}V_{n\times r}=U_{m\times r}\Sigma_{r\times r} \end{matrix}$$

  This equation is what we call Reduced SVD

We have seen that we can write any $m\times n$ matrix $A$ as $AV=U\Sigma$ where $V$ and $U$ are Orthonormal matrix.
Now the real challange is to find these $V$ and $U$ Orthonormal matrix.
Once we got those $V$ and $U$ Orthonormal matrix then we can find $A$ as,
$AV=U\Sigma$
$A=U\Sigma V^{-1}$
And because $V$ is an orthogonal matrix so we know that $V^{-1}=V^T$
To achieve it we need $V$ to be square matrix so we have to use Full SVD method, then we get

danger

$$\begin{matrix} A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V_{n\times n}^{T} \end{matrix}$$

Everything looks good but how to find these $V$ and $U$ Orthonormal matrix.

info

IDEA: to find the $V$ and $U$ are the Matrices $A^TA$ and $AA^T$

info

• Row space of $A$ is same as Row space of $A^TA$.

• It is easy to find the basis for Row space of $A^TA$, so rather than finding basis for Row space of $A$ we will find basis for Row space of $A^TA$*

Explanation:

$A_{m\times n}=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix}$
Let's rewrite $A^TA$
$A^TA=A^T\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix}$

Here we can see that we are mapping the row vectors of $A$ onto the Row Space of $A^T$.

And if $\text{Rank}(A)=r$ then $\Rightarrow \text{Rank}(A^T)=r$ so $A$ and $A^T$ both are $r$-dimensions Row Space.

So when we map row vector of $A$ onto the Row Space of $A^T$ then the resulting Row Space also has $r$-dimensions, so we can say that $\text{Rank}(A^TA)=r$

Now we can say that Row Space of $A$ is same as Row Space of $A^TA$.

$(A^TA)^T=A^TA \Rightarrow A^TA$ is symmetric matrix, so
Row Space of $A^TA=$ Column Space of $A^TA=$ Row Space of $A$

info

• Column Space of $A$ is same as Column Space of $AA^T$

• It is easy to find the basis for Column Space of $AA^T$, so rather than finding basis for Column Space of $A$ we will find basis for Column Space of $AA^T$*

Explanation:
$A^T_{m\times n}=\begin{bmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \\ \end{bmatrix}$
Let's rewrite $AA^T$
$AA^T=A\begin{bmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \\ \end{bmatrix}$

Here we can see that we are mapping the column vectors of $A^T$ onto the Column Space of $A$.

And if $\text{Rank}(A)=r$ then $\Rightarrow \text{Rank}(A^T)=r$ so $A$ and $A^T$ both are $r$-dimensions Column Space.

So when we map column vector of $A^T$ onto the Column Space of $A$ then the resulting Column Space also has $r$-dimensions, so we can say that $\text{Rank}(AA^T)=r$

Now we can say that Column Space of $A$ is same as Column Space of $AA^T$.

$(AA^T)^T=AA^T \Rightarrow AA^T$ is symmetric matrix, so
Column Space of $AA^T=$ Row Space of $AA^T=$ Column Space of $A$

Finding orthonormal Row vectors$(V)$ for matrix $A$

We discussed that Row space of $A$ is same as Row space of $A^TA$.
So we need to find orthonormal Row vectors for matrix $A^TA$.

$A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V_{n\times n}^{T}$
$(\Sigma^T_{m\times n}=\Sigma_{n\times m})$
$\Rightarrow (A^T)_{n\times m} = V_{n\times n}\Sigma_{n\times m}U_{m\times m}^{T}$

$$\Rightarrow (A^T)_{n\times m}A_{m\times n} = V_{n\times n}\Sigma_{n\times m} \underbrace{U_{m\times m}^{T} U_{m\times m}}_{=\mathcal{I}_m} \Sigma_{m\times n}V_{n\times n}^{T}$$

$$\Sigma_{n\times m}\Sigma_{m\times n}= \underbrace{\begin{bmatrix} \begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m \\ \end {bmatrix}_{m\times m} \\ \mathbf{0}_{(n-m)\times m} \end {bmatrix}}_{ \Sigma_{n\times m} } \underbrace{\begin{bmatrix} \begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m \\ \end {bmatrix}_{m\times m} & \mathbf{0}_{m\times (n-m)} \end {bmatrix}}_{ \Sigma_{m\times n} }$$

$$\Sigma_{n\times m}\Sigma_{m\times n}= \underbrace{\begin{bmatrix} \begin{bmatrix} \sigma_1^2 & & & \huge0 \\ & \sigma_2^2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m^2 \\ \end {bmatrix}_{m\times m} & \mathbf{0}_{m\times (n-m)} \\ \mathbf{0}_{(n-m)\times m} & \mathbf{0}_{(n-m)\times (n-m)} \\ \end{bmatrix}}_{ \Sigma^2_{n\times n}} = \Sigma^2_{n\times n}$$

$$\Sigma^2_{n\times n}= \begin{bmatrix} \begin{bmatrix} \sigma_1^2 & & & \huge0 \\ & \sigma_2^2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m^2 \\ \end {bmatrix}_{m\times m} & \mathbf{0}_{m\times (n-m)} \\ \mathbf{0}_{(n-m)\times m} & \mathbf{0}_{(n-m)\times (n-m)} \\ \end{bmatrix}_{n\times n}$$

$\Rightarrow (A^T)_{n\times m}A_{m\times n} = V_{n\times n}\Sigma^2_{n\times n}V_{n\times n}^{T}$
Those $3$ $\mathbf{0}$ matrices are interesting,

• $\mathbf{0}_{m\times (n-m)}$
• $\mathbf{0}_{(n-m)\times m}$
• $\mathbf{0}_{(n-m)\times (n-m)}$ Remember that in Full SVD we said that $\text{Rank}(A)=m$ so there must be $n-m$ dependent row vectors. and these $\mathbf{0}$ matrices are negating those dependent vectors.
  

info

Remember $[A=Q\Lambda Q^T]$ where $A$ is symmetric matrix.

$A^TA$ is a symmetric matrix, so

info

Columns of $V$ are eigenvectors of matrix $A^TA$, and $\sigma_i^2$ are the $i^{th}$ eigenvalue of matrix $A^TA$

Finding orthonormal Column Vectors$(U)$ for matrix $A$

We discussed that Column Space of $A$ is same as Column Space of $AA^T$.
So we need to find orthonormal Column vectors for matrix $AA^T$.

$A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V_{n\times n}^{T}$
$(\Sigma^T_{m\times n}=\Sigma_{n\times m})$
$\Rightarrow (A^T)_{n\times m} = V_{n\times n}\Sigma_{n\times m}U_{m\times m}^{T}$
$\Rightarrow A_{m\times n}(A^T)_{n\times m} = U_{m\times m}\Sigma_{m\times n} \underbrace{V_{n\times n}^{T} V_{n\times n}}_{=\mathcal{I}_n} \Sigma_{n\times m}U_{m\times m}^{T}$

$$\Sigma_{m\times n}\Sigma_{n\times m}= \underbrace{\begin{bmatrix} \begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m \\ \end {bmatrix}_{m\times m} & \mathbf{0}_{m\times (n-m)} \end {bmatrix}}_{ \Sigma_{m\times n} } \underbrace{\begin{bmatrix} \begin{bmatrix} \sigma_1 & & & \huge0 \\ & \sigma_2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m \\ \end {bmatrix}_{m\times m} \\ \mathbf{0}_{(n-m)\times m} \end {bmatrix}}_{ \Sigma_{n\times m} }$$

$$\Sigma_{n\times m}\Sigma_{m\times n}= \underbrace{\begin{bmatrix} \sigma_1^2 & & & \huge0 \\ & \sigma_2^2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m^2 \\ \end{bmatrix}}_{ \Sigma^2_{m\times m}} = \Sigma^2_{m\times m}$$

$$\Sigma^2_{m\times m}= \begin{bmatrix} \sigma_1^2 & & & \huge0 \\ & \sigma_2^2 & & \\ & & \ddots & \\ \huge0 & & & \sigma_m^2 \\ \end{bmatrix}_{m\times m}$$

$\Rightarrow A_{m\times n}(A^T)_{n\times m} = U_{m\times m}\Sigma^2_{m\times m}U_{m\times m}^{T}$
This time there isn't any $\mathbf{0}$ matrix, because as we discussed, in Full SVD $\text{Rank}(A)=m$ so all columns vectors and row vectors of $U$ are independent.

info

Remember $[A=Q\Lambda Q^T]$ where $A$ is symmetric matrix.

$AA^T$ is a symmetric matrix, so

info

Columns of $U$ are eigenvectors of matrix $AA^T$, and $\sigma_i^2$ are the $i^{th}$ eigenvalue of matrix $AA^T$